Solución. Práctica 1

Lo primero de todo es colocar en un dibujo los datos que tenemos, para así poder interpretar el problema mas fácilmente

Como la pendiente de la rampa debe ser del 35% esto implica que de cada 100 metros que avanzemos en horizontal subimos 35 metros en vertical. De esta manera podemos plantear la resolución del problema como una relación entre dos triángulos de la siguiente forma:

Por un lado tenemos un triángulo rectángulo de base "m" 100 cm y de altura "n" 35 cm, y por otro lado tenemos un triángulo del que desconocemos la base "x" y sabemos la altura "h" 60 cm

Para plantear la relación usamos el Teorema de Tales y nos quedaría la siguiente expresión:

m/n = x/h        100/35 = x/60      x= 171,4 cm

Si queréis resolverlo de forma gráfica podéis hacerlo de la siguiente manera:

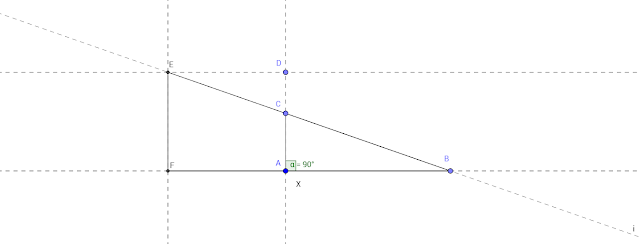
1.-Trazamos dos rectas perpendiculares, sobre la recta horizontal y empezando en A colocamos un segmento de 100 cm AB y sobre la recta vertical de 35 cm AC. Ya tenemos establecido nuestra pendiente del 35%, es decir, el primer triángulo (ABC).

2.- Sabemos que la altura de nuestro triángulo solución es de 60 cm, por lo tanto colocamos esa altura en perpendicular desde A y obtenemos AD, ahora tenemos que realizar un triángulo semejante al anterior.

3.- Desde D trazamos una recta paralela a AB y prolongamos el lado CB hasta que corte con la recta que acabamos de realizar, al punto de corte le llamamos E.

4.-Desde E trazamos una recta perpendicular a AB y donde corte con AB será el punto F. El triángulo FBE es el triángulo solución, es decir el lado FB, que corresponde con la base, es la distancia que estábamos buscando.

¿Qué tal os ha ido? ¿ Habéis acertado? :)